薄膜干渉の式
状況設定
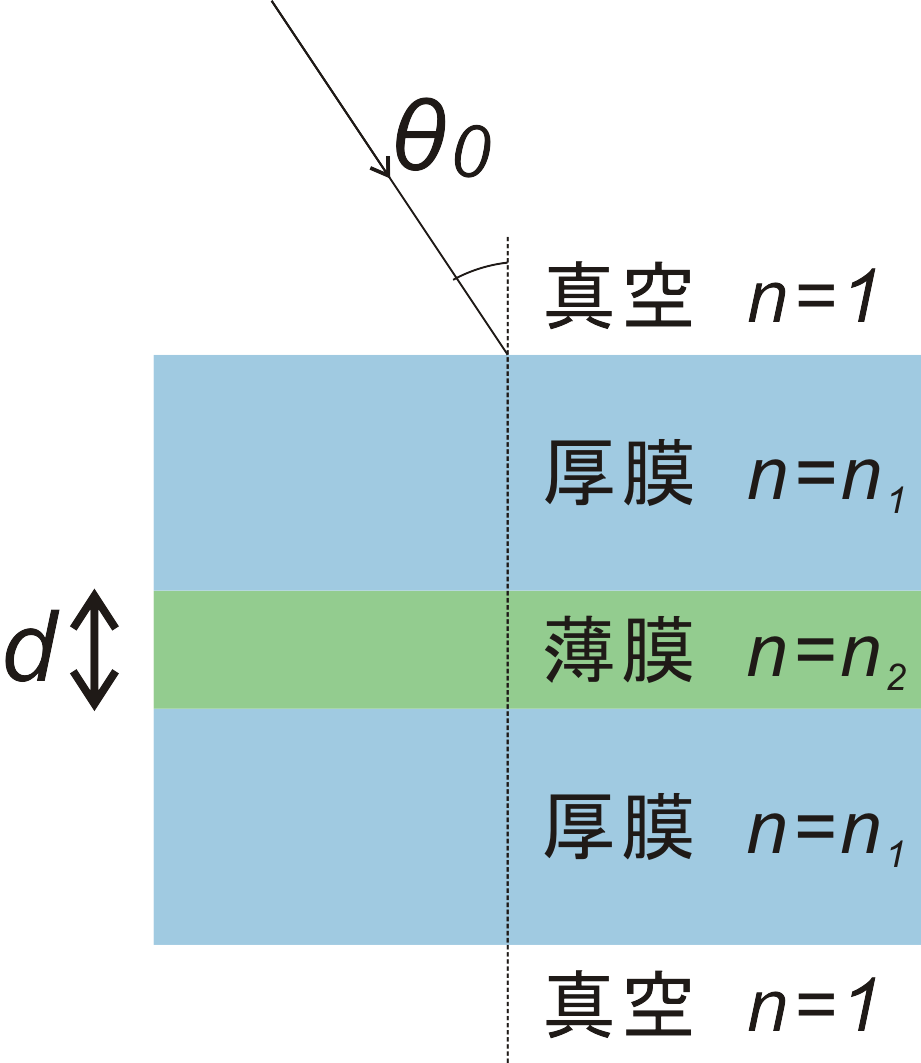
屈折率 \(n_1\) の吸収の無い2枚の厚膜の間に吸収のある屈折率 \(n_{2}\) の薄膜が挟まっている。
この試料を屈折率1.0の空気や真空中に置き、垂線からの入射角 \(\theta_{0}\) で入射する。
いずれの物質も導電性はないとし、磁性も無視できるとします。
すると、 \(\rho=0,~ j=0,~ \mu=\mu_{0}\) とおけるので、マクスウェル方程式は以下の様に書き直せる。
\[\begin{equation}
\left\{
\begin{array}{l}
div D = 0 \\
rot E = -\frac{dB}{dt} \\
div B = 0 \\
rot H = \frac{dD}{dt} \\
D=\varepsilon_{r} \varepsilon_{0} E~~~~~(\varepsilon_{r}=1, n_{1}^{2}~{\rm or}~ n_{2}^{2})\\
B=\mu_{0} H
\end{array}
\right.
\end{equation}\]
波動方程式と平面波解
数学公式 \(rot ~rot E =grad ~div - \Delta ~\) を用いると、上のマクスウェル方程式から容易に波動方程式が導かれる。
\[\begin{equation}
(\Delta - \mu_{0}\varepsilon_{0}\varepsilon{r} \frac{\partial ^{2}}{\partial t^{2}}) \left(\begin{array}{c} E\\ H\end{array}\right)=0
\end{equation}\]
これを満たす平面波解を考えてみる。
時間空間依存性を \(\exp({i\omega t-ikz})\) とおく事にする。
これは、z方向に進行する平面波を意味する。
また、屈折率は一般に複素数なので、ここでは \(\hat{n}\) と表す。
波動方程式を満たすには、
\[\begin{equation}
\omega/k=c/\sqrt{\varepsilon_{r}}=c/\hat{n}
\end{equation}\]
である事が分かる。
誘電率の等方性を仮定すると、電場、磁場はz成分を持たない事がマクスウェル方程式から求められる。
電場の方向をx方向とすると、磁場の方向はy方向となり、磁場と電場の間には
\[\begin{equation}
H=\sqrt{\frac{\varepsilon}{\mu}}E=\sqrt{\varepsilon_{r} }\sqrt{\frac{\varepsilon_{0}}{\mu_{0}}}E=\hat{n} \sqrt{\frac{\varepsilon_{0}}{\mu_{0}}}E
\end{equation}\]
という関係がある。
電磁波の空間対称性
真空中、媒質1中では吸収がないので、入射光を平面波とするとこれらの物質中での光は平面波とみなすことが出来る
しかし、吸収媒質2の中の光は前節で述べた様な平面波ではない。
この事はこの系を理解する上での最大のポイントなので、十分に注意する必要がある。
平面波が媒質1から吸収媒質2に角度 \(\theta_{1}\) で入射した場合、どの様な対称性が要請されるのか考える。
媒質1、2の厚みをどちらも一様とし、垂線方向にz軸をとる。
また、入射面内にx軸、それと垂直にy軸をとる。
すると、明らかにy軸方向には並進対称性がある。
また、媒質1中での光の波長を \(\lambda_{1}\) とおくと、この系はx軸方向に \(\lambda_{1}/\sin{\theta_{1}}\) の周期性がある。
この周期性は全媒質中で成立していて、真空と媒質1との境界ではSnellの法則
\[\begin{equation}
\sin{\theta_{0}}=n_{1}\sin{\theta_{1}}
\end{equation}\]
として表せる。
今度はこれを波数で表現する。
真空中での角波数(angular wavenumber)を \(k_{0}\) と書くと、
そのx成分は \(k_{x}=k_{0}\sin{\theta_{0}}\) となり、全媒質中での電磁波のx依存性が
\[ \begin{equation}
\exp{(-i k_{x}x)}
\end{equation}で表せることになる。\]
ただし、時間依存性は前節と同様に
\[ \begin{equation}
\exp{(i \omega t)}
\end{equation}\]
を仮定している。
薄膜中での電磁波
ここから、電磁波(光)を二つの偏光成分に分けて考える。
一つは電場がy成分を向いている成分、もう一つは磁場がy成分を向いている成分。
前者をS波、後者をP波と呼ぶ。
S波の電場を \(E_{y}\) 、P波の磁場を \(H_{y}\) と置く。
これらは波動方程式を満たすので、
\[\begin{equation}
(\Delta + \mu_{0}\varepsilon_{0}\varepsilon_{r}\omega^{2}) \left(\begin{array}{c} E_{y}\\ H_{y}\end{array}\right)=0
\end{equation}\]
が成り立つ。
前節で述べた事に注意すると、電磁波の空間依存性は
\[\begin{equation}
\exp{[-i (k_{x}x+k_{z}z)]}
\end{equation}\]
と表す事ができる。
\(k_{z}\) は今のところ未知の複素数なので、これを計算する。
- ここで、薄膜中の複素屈折率を \(n_{2}\) とすると、
- \(\mu_{0}\varepsilon_{0}\varepsilon_{r}\omega^{2}=n_{2}^{2}k_{0}^{2}\) と書き直せる事に注意すると、波動方程式から
\[\begin{equation}
kz=\pm \sqrt{n_{2}^{2}k_{0}^{2}-k_{x}^{2}}=\pm k_{0}\sqrt{n_{2}^{2}-\sin^{2}{\theta_{0}}}
\end{equation}\]
となり、二つの解が得られる。
これは薄膜中を干渉する上下方向の二つの電磁波を表わしている。
そこでnotationを改め、以下の様にまとめる。
\[\begin{equation}
\left\{
\begin{array}{l}
\left( \begin{array}{c} E_{+}\\ H_{+}\end{array}\right) \propto \exp{[-i (k_{x}x + k_{z}z)]}\\
\left( \begin{array}{c} E_{-}\\ H_{-}\end{array}\right) \propto \exp{[-i (k_{x}x - k_{z}z)]}\\
k_{x}=k_{0}\sin{\theta_{0}}\\
kz=k_{0}\sqrt{n_{2}^{2}-\sin^{2}{\theta_{0}}}
\end{array}
\right.
\end{equation}\]
薄膜中の電磁波は上記の空間依存性を持つ事が分かったが、その振幅はまだ明らかになっていない。
残った計算は、厚い物質と真空、薄膜と厚い物質の間での境界条件を満たすようにそれぞれの領域での電磁場の振幅を決める事である。
その為に薄膜中の電磁場の残りの成分を計算しておく必要がある。
マクスウェル方程式に代入する事で計算すると、以下のようになる。
|
\[\text{電場}\]
|
\[\text{磁場}\]
|
|---|
\[S波(+)\]
|
\[(0, E_+ ,0)\]
|
\[(-\frac{k_z}{\omega \mu}E_+,~ 0,
~\frac{k_x}{\omega \mu}E_+ )\]
|
\[S波(-)\]
|
\[(0, E_- ,0)\]
|
\[(\frac{k_z}{\omega \mu}E_-,~ 0,
~\frac{k_x}{\omega \mu}E_- )\]
|
\[P波(+)\]
|
\[(\frac{k_z}{\omega \varepsilon}H_+,
~0,~-\frac{k_x}{\omega \varepsilon}H_+)\]
|
\[(0, H_+, 0)\]
|
\[P波(-)\]
|
\[(-\frac{k_z}{\omega \varepsilon}H_-,
~0,~-\frac{k_x}{\omega \varepsilon}H_-)\]
|
\[(0, H_- ,0)\]
|
境界条件の定式化の方法
境界条件を実際に計算する方法には2通りの方法がある。
- 各領域の電磁場の振幅を変数におき、各界面で満たす条件を連立する方法。
- 光線が次々と反射、屈折する様子を想定し、無限級数の和として電磁場を得る方法。
系が複雑になると後者の方が計算が簡単になるのかもしれないが、今の様な簡単な系ではどちらの方法も同程度の複雑さだと思われる。
多くの教科書では後者を用いた説明が多いようである。
連立による計算
各領域の電磁場振幅
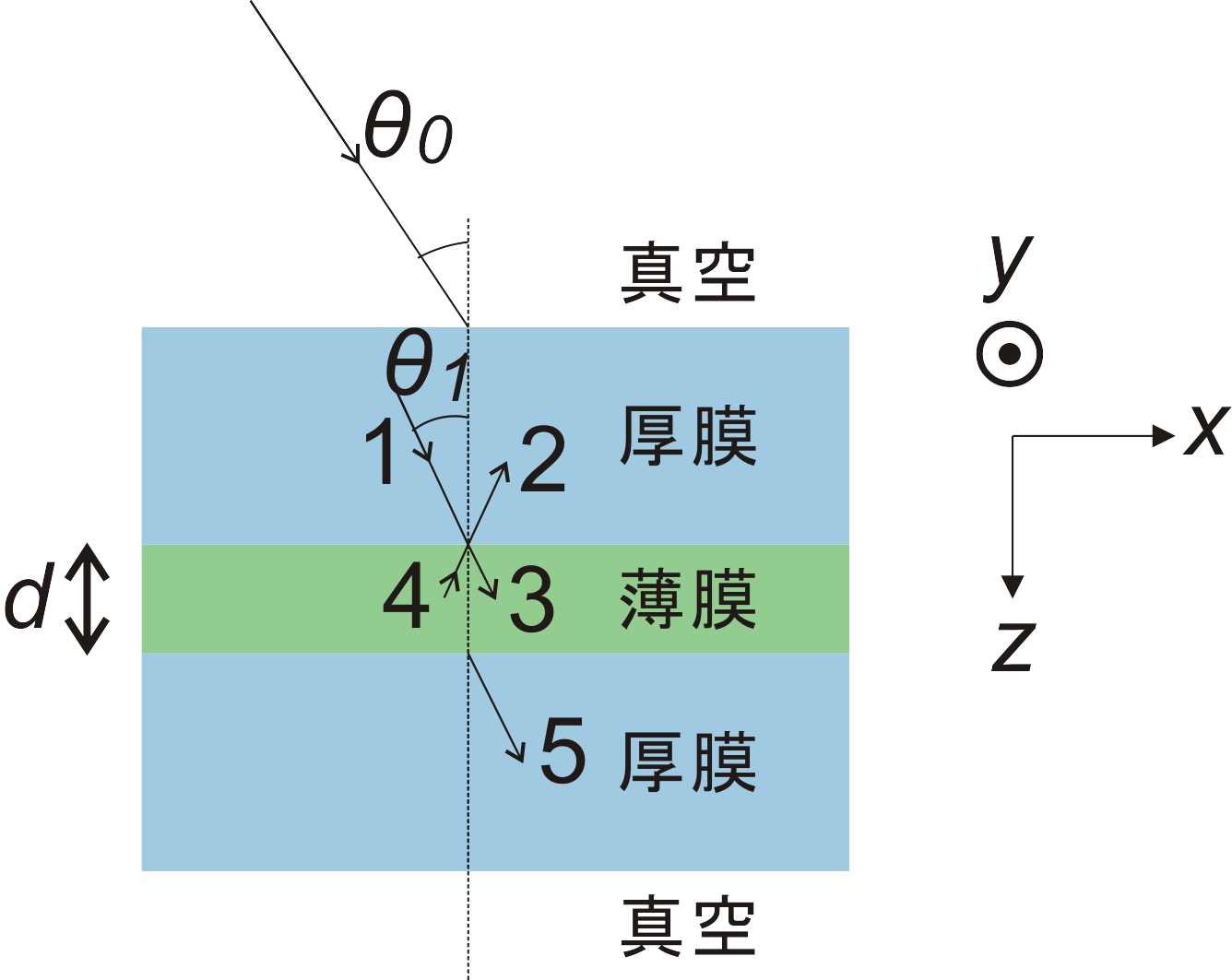
図のように各領域の電磁場振幅に番号を振る。ただし、1から4については薄膜への入射面でのある1点で定義し、
5については、その点の直下に位置する薄膜の透過面内の点で定義する事にする。
S波については電場のy成分として \((E_{1}, E_{2}, E_{3}, E_{4}, E_{5})\) とし、
P波については磁場のy成分として \((H_{1}, H_{2}, H_{3}, H_{4}, H_{5})\) とする。
ただし、薄膜中の光は平面波ではないので、3、4の矢印はz方向の角波数が \(+k_{z}\) のもの
\((E_+,~ H_+)\) と
\(-k_{z}\) のもの
\((E_-,~ H_-)\) に対応している。
これらの各振幅が満たすべき関係について考えていく。
電場の接線成分連続
\[\begin{equation}
\begin{array}{ccl}
\text{S波} & \text{薄膜上面} & E_{1}+E_{2}=E_{_3}+E_{4} \\
& \text{薄膜下面} & E_{3} \exp{(-ik_{z}d)}+E_{4} \exp{(ik_{z}d)}=E_{5} \\
\text{P波} & \text{薄膜上面} & \sqrt{\frac{\mu_{0}}{\varepsilon_{1}}}H_{1}\cos{\theta _{1}}-\sqrt{\frac{\mu_{0}}{\varepsilon_{1}}}H_{2}\cos{\theta _{1}}
=\frac{k_{z}}{\omega \varepsilon _{2}}H_{_3}-\frac{k_{z}}{\omega \varepsilon _{2}}H_{4} \\
& \text{薄膜下面} & \frac{k_{z}}{\omega \varepsilon _{2}}H_{3} \exp{(-ik_{z}d)}-\frac{k_{z}}{\omega \varepsilon _{2}}H_{4} \exp{(ik_{z}d)}
=\sqrt{\frac{\mu_{0}}{\varepsilon_{1}}}H_{5}\cos{\theta_{1}}
\end{array}
\end{equation}\]
電束密度の法線成分連続
\[\begin{equation}
\left(
\begin{array}{ccl}
\text{S波} & \text{薄膜上面} & 0=0 \\
& \text{薄膜下面} & 0=0 \\
\text{P波} & \text{薄膜上面} & -\sqrt{\varepsilon_{1}\mu_{0}}H_{1}\sin{\theta _{1}}-\sqrt{\varepsilon_{1}\mu_{0}}H_{2}\sin{\theta _{1}}
=-\frac{k_{x}}{\omega}H_{_3}-\frac{k_{x}}{\omega}H_{4} \\
& \text{薄膜下面} & -\frac{k_{x}}{\omega}H_{3} \exp{(-ik_{z}d)}-\frac{k_{x}}{\omega}H_{4} \exp{(ik_{z}d)}
=-\sqrt{\varepsilon_{1}\mu_{0}}H_{5}\sin{\theta_{1}}
\end{array}
\right)
\end{equation}\]
磁場の接線成分連続
\[\begin{equation}
\begin{array}{ccl}
\text{S波} & \text{薄膜上面} & -\sqrt{\frac{\varepsilon _{1}}{\mu_{0}}}E_{1}\cos{\theta_{1}}+\sqrt{\frac{\varepsilon _{1}}{\mu_{0}}}E_{2}\cos{\theta_{1}}
=-\frac{k_{z}}{\omega \mu_{0}}E_{_3}+\frac{k_{z}}{\omega \mu_{0}}E_{4} \\
& \text{薄膜下面} & -\frac{k_{z}}{\omega \mu_{0}}E_{3} \exp{(-ik_{z}d)}+\frac{k_{z}}{\omega \mu_{0}}E_{4} \exp{(ik_{z}d)}
=-\sqrt{\frac{\varepsilon _{1}}{\mu_{0}}}E_{5}\cos{\theta_{1}} \\
\text{P波} & \text{薄膜上面} & H_{1}+H_{2}=H_{_3}+H_{4} \\
& \text{薄膜下面} & H_{3} \exp{(-ik_{z}d)}+H_{4} \exp{(ik_{z}d)}=H_{5}
\end{array}
\end{equation}\]
磁束密度の法線成分連続
\[\begin{equation}
\left(
\begin{array}{ccl}
\text{S波} & \text{薄膜上面} & \sqrt{\frac{\varepsilon _{1}}{\mu_{0}}}E_{1}\sin{\theta_{1}}+\sqrt{\frac{\varepsilon _{1}}{\mu_{0}}}E_{2}\sin{\theta_{1}}
=\frac{k_{x}}{\omega \mu_{0}}E_{_3}+\frac{k_{x}}{\omega \mu_{0}}E_{4} \\
& \text{薄膜下面} & \frac{k_{x}}{\omega \mu_{0}}E_{3} \exp{(-ik_{z}d)}+\frac{k_{x}}{\omega \mu_{0}}E_{4} \exp{(ik_{z}d)}
=\sqrt{\frac{\varepsilon _{1}}{\mu_{0}}}E_{5}\sin{\theta _{1}} \\
\text{P波} & \text{薄膜上面} & 0=0 \\
& \text{薄膜下面} & 0=0
\end{array}
\right)
\end{equation}\]
有意な式
上記の16個の式のうち、括弧で囲んだ式は無視してよい。
なぜなら、 \(0=0\) は自明だし、他の4式は
\(k_x = \omega \sqrt{\mu_0 \varepsilon_1}\sin{\theta_1}\)
を代入すれば他の式と等価になるからである。
結局残った8式が有意な式であり、未知数は10個ある。入射光振幅 \(E_1,~H_1\) を決めれば残りが決まる。
また、入射光振幅に対する他の光の振幅の比は計算できる事になる。
また、振幅比ではなく、強度比が求まれば十分な事も多い。
行列表現
上記の8式を注意深く書き直すと、以下の様な行列表現に書き直す事ができる。
\[\begin{equation}
\left(
\begin{array}{cccc}
-1 & 1 & 1 & 0 \\
0 & \exp{(-ik_{z}d)} & \exp{(ik_{z}d)} & -1\\
n_{1}\cos{\theta_{1}} & \frac{k_{z}}{k_{0}} & -\frac{k_{z}}{k_{0}} & 0 \\
0 & -\frac{k_{z}}{k_{0}} \exp{(-ik_{z}d)} & \frac{k_{z}}{k_{0}} \exp{(ik_{z}d)} & n_{1}\cos{\theta_{1}}
\end{array}
\right)
\left(
\begin{array}{cccc}
E_{2} \\
E_{3} \\
E_{4} \\
E_{5}
\end{array}
\right)
=
\left(
\begin{array}{cccc}
1 \\
0 \\
n_{1}\cos{\theta_{1}} \\
0
\end{array}
\right)
E_{1}
\end{equation}\]
\[\begin{equation}
\left(
\begin{array}{cccc}
-1 & 1 & 1 & 0 \\
0 & \exp{(-ik_{z}d)} & \exp{(ik_{z}d)} & -1\\
n_{1}\cos{\theta_{1}} & \frac{n_{1}^{2}k_{z}}{n_{2}^{2}k_{0}} & -\frac{n_{1}^{2}k_{z}}{n_{2}^{2}k_{0}} & 0 \\
0 & -\frac{n_{1}^{2}k_{z}}{n_{2}^{2}k_{0}} \exp{(-ik_{z}d)} & \frac{n_{1}^{2}k_{z}}{n_{2}^{2}k_{0}} \exp{(ik_{z}d)} & n_{1}\cos{\theta_{1}}
\end{array}
\right)
\left(
\begin{array}{cccc}
H_{2} \\
H_{3} \\
H_{4} \\
H_{5}
\end{array}
\right)
=
\left(
\begin{array}{cccc}
1 \\
0 \\
n_{1}\cos{\theta_{1}} \\
0
\end{array}
\right)
H_{1}
\end{equation}\]
光線を順に追う計算
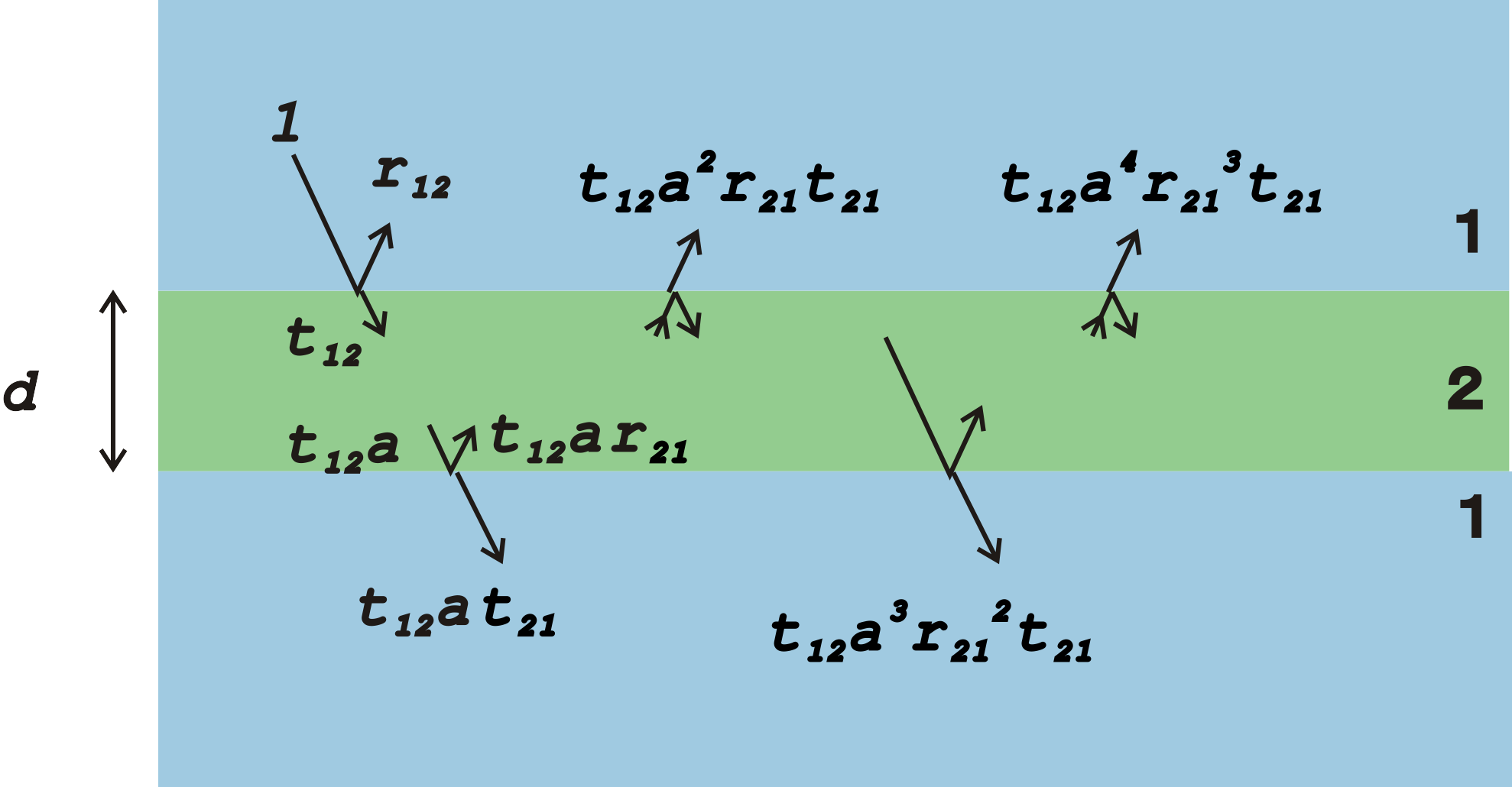
図のように薄膜を2、厚膜を1として、光線が各界面を通過する際の反射と透過を考える。
ここでは簡単の為に、入射光の振幅を1としている。
各界面での振幅透過率と振幅反射率を以下の様に定義しておく。
- t 12
- 厚膜から薄膜へ入射した際の振幅透過率
- r 12
- 厚膜から薄膜へ入射した際の振幅反射率
- t 21
- 薄膜から厚膜へ入射した際の振幅透過率
- r 21
- 薄膜から厚膜へ入射した際の振幅反射率
また、薄膜を通過する際の振幅と位相の変化を a とおく。
これらの多光束が干渉したものが観測されるので、これらの無限級数の和を計算すれば良い。
従って、観測される振幅反射率( r )と透過率( t )は
\[ \begin{equation}
r=r_{12}+r_{21}t_{12}t_{21}a^{2}+r_{21}^{3}t_{12}t_{21}a^{4}+\dots=r_{12}+r_{21}t_{12}t_{21}\frac{a^{2}}{1-r_{21}^{2}a^{2}} \\
t=t_{12}t_{21}a+t_{12}t_{21}r_{21}^{2}a^{3}+\dots=t_{12}t_{21}\frac{a}{1-r_{21}^{2}a^{2}}
\end{equation}\]
a は何か?
先の式に現われた a はどう評価すれば良いだろうか。
薄膜中を斜めに進行する波数ベクトルを考える必要があるだろうか?
光線を考えると言ったが、干渉は同じ位置の波同士で起こるはずなので、x,y方向の移動は考えてはいけない。
つまり、z方向の移動のみ考慮し、 \(a=\exp{(-i k_z d)}\) とすれば良い。
厚膜から薄膜への入射
次に、個々の振幅透過率と振幅反射率を計算する。
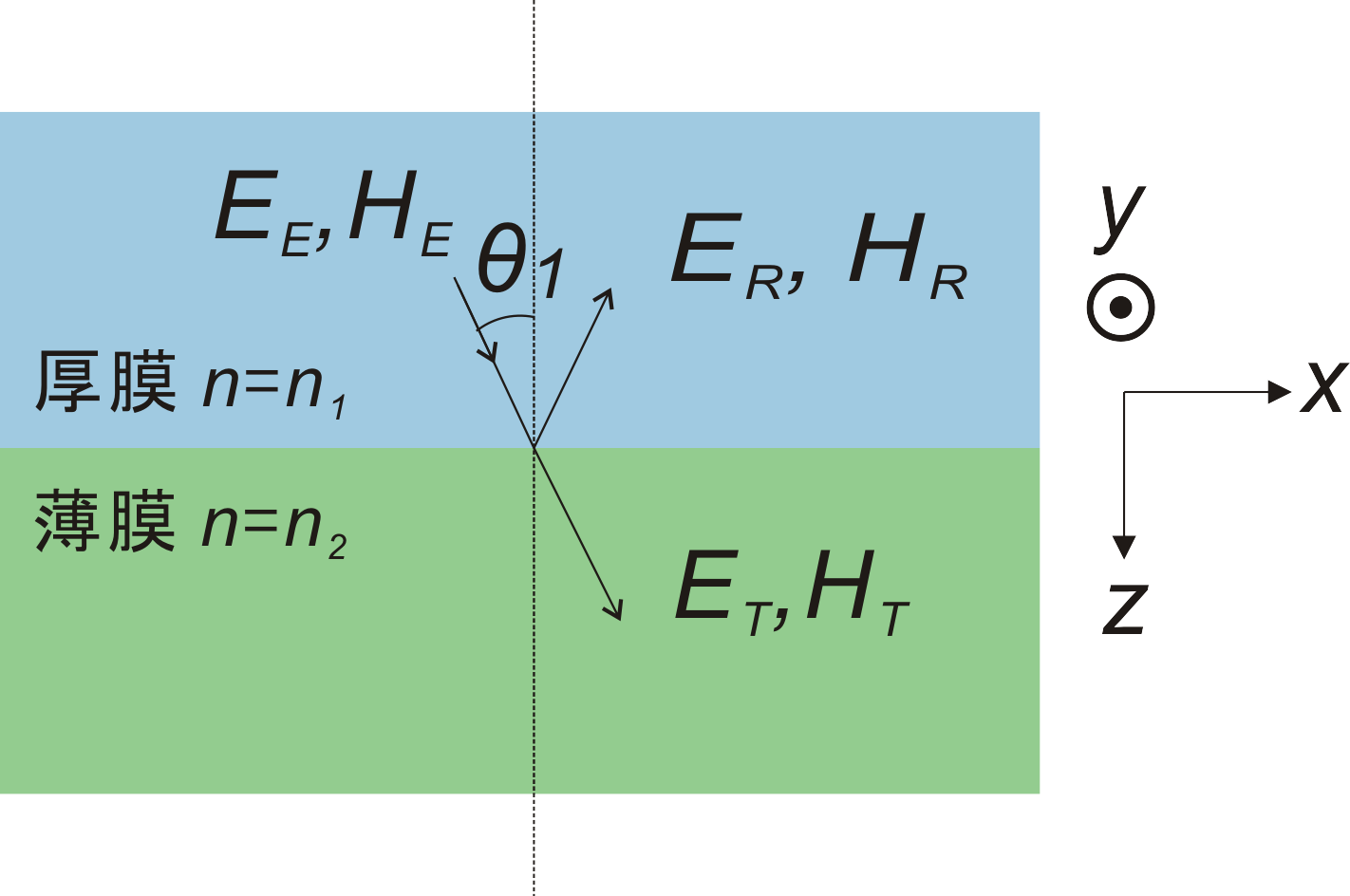
図のように、S波の場合には電場を定義し、P波の場合には磁場を定義する。定義の向きは全て図のy方向である。
境界条件として、x方向とy方向の電場、磁場の連続条件を考える。
(詳細は省略するが、これらを満たすように解を決めれば、残りの境界条件は自動的に満たされる事が確認できる。)
得られる式は以下の通りである。
\[ \begin{equation}
\left\{
\begin{array}{l}
E_{E}+E_{R}=E_{T} \\
H_{E}+H_{R}=H_{T} \\
\sqrt{\frac{\varepsilon_{1}}{\mu_{0}}}\cos \theta_{1} (-E_{E}+E_{R})=-\frac{k_{z}}{\omega \mu_{0}}E_{T} \\
\sqrt{\frac{\mu_{0}}{\varepsilon_{1}}}\cos \theta_{1} (H_{E}-H_{R})=\frac{k_{z}}{\omega \varepsilon_{2}}H_{T}
\end{array}
\right.
\end{equation}\]
ここで、 \(\sqrt{\frac{\varepsilon_{1}}{\mu_{0}}}=\frac{n_{1}\varepsilon_{0}}{c}\)、
\(k_{z}=k_{0}\sqrt{n_{2}^{2}-\sin ^{2} \theta_{0}}\)
などに注意して整理すると、
\[ \begin{equation}
\def\A{n_{1}\cos \theta_{1}}
\def\B{\sqrt{n_{2}^{2}-\sin ^{2} \theta_{0}}}
\def\C{{\cos \theta_{1}}/{n_{1}}}
\def\D{{\sqrt{n_{2}^{2}-\sin ^{2} \theta_{0}}}/{n_{2}^{2}}}
r_{12}^{S}=\frac{E_{R}}{E_{E}}=\frac{\A-\B}{\A+\B} \\
t_{12}^{S}=\frac{E_{T}}{E_{E}}=\frac{2\A}{\A+\B} \\
r_{12}^{P}=\frac{H_{R}}{H_{E}}=\frac{\C-\D}{\C+\D} \\
t_{12}^{P}=\frac{H_{T}}{H_{E}}=\frac{2\C}{\C+\D}
\end{equation}\]
となる。
薄膜から厚膜への入射
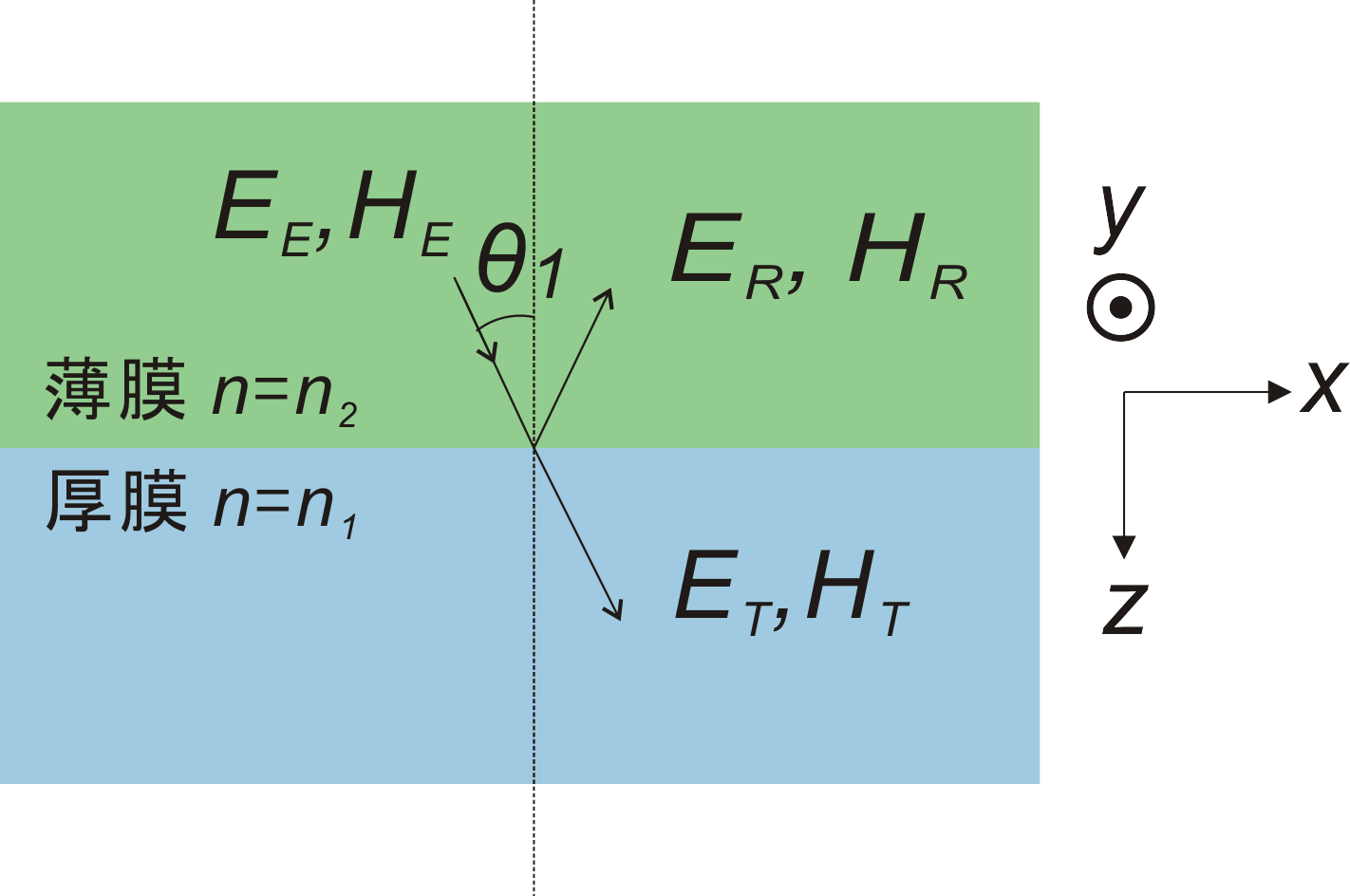
今度も図のように、S波の場合には電場を定義し、P波の場合には磁場を定義する。定義の向きは全て図のy方向である。
境界条件として、x方向とy方向の電場、磁場の連続条件を考える。
得られる式は以下の通りである。
\[ \begin{equation}
\left\{
\begin{array}{l}
E_{E}+E_{R}=E_{T} \\
H_{E}+H_{R}=H_{T} \\
\frac{k_{z}}{\omega \mu_{0}}(-E_{E}+E_{R})=-\sqrt{\frac{\varepsilon_{1}}{\mu_{0}}}\cos \theta_{1}E_{T} \\
\frac{k_{z}}{\omega \varepsilon_{2}}(H_{E}-H_{R})=\sqrt{\frac{\mu_{0}}{\varepsilon_{1}}}\cos \theta_{1}H_{T}
\end{array}
\right.
\end{equation}\]
これも同様に整理すると、
\[ \begin{equation}
\def\A{n_{1}\cos \theta_{1}}
\def\B{\sqrt{n_{2}^{2}-\sin ^{2} \theta_{0}}}
\def\C{{\cos \theta_{1}}/{n_{1}}}
\def\D{{\sqrt{n_{2}^{2}-\sin ^{2} \theta_{0}}}/{n_{2}^{2}}}
r_{21}^{S}=\frac{E_{R}}{E_{E}}=\frac{\B-\A}{\B+\A} = -r_{12}^{S}\\
t_{21}^{S}=\frac{E_{T}}{E_{E}}=\frac{2\B}{\B+\A} \\
r_{21}^{P}=\frac{H_{R}}{H_{E}}=\frac{\D-\C}{\D+\C} = r_{12}^{P}\\
t_{21}^{P}=\frac{H_{T}}{H_{E}}=\frac{2\D}{\D+\C}
\end{equation}
となる。\]
解
境界条件を解いて得られる解を示す。
これは行列で表現された連立方程式を解いても良いし、無限級数の解に各領域での反射率、透過率等を代入しても良い。
全体の複素共役も又解である。
複素屈折率の虚部を正にするか、
負にするか(時間依存性を \(\exp{(-i\omega t)}\) にするか、 \(\exp{(i\omega t)}\) にするか)は流儀の問題である。
厚い物質と真空との間の反射を考慮するともう少し複雑になる。
その場合には実験条件によって様々なケースを考える必要がある。
複素振幅透過率
薄膜に入射した電場、磁場と薄膜から透過した電場、磁場の複素振幅の比である。
\[ \begin{equation}
\left\{
\def\nAcosineA{\sqrt{n_{1}^{2}-\sin ^{2} \theta_{0}}}
\def\nBcosineB{\sqrt{n_{2}^{2}-\sin ^{2} \theta_{0}}}
\def\nAsq{n_{1}^{2}}
\def\nBsq{n_{2}^{2}}
\begin{array}{l}
n_{1}{\rm :~~real}\\
n_{2}=n-i\kappa\\
k_{0}{\rm :~~angular~~wavenumber~~in~~vacuum}\\
k_{z}=k_{0}\nBcosineB\\
t_{s}=\frac{E5}{E1}=\frac{4 \nAcosineA \nBcosineB}{(\nAcosineA+\nBcosineB)^{2}\exp{(ik_{z}d)} - (\nAcosineA-\nBcosineB)^{2}\exp{(-ik_{z}d)}}\\
t_{p}=\frac{H5}{H1}=\frac{4 \nAsq \nBsq \nAcosineA \nBcosineB}{(\nBsq \nAcosineA+\nAsq \nBcosineB)^{2}\exp{(ik_{z}d)} - (\nBsq \nAcosineA - \nAsq \nBcosineB)^{2
}\exp{(-ik_{z}d)}}
\end{array}
\right.
\end{equation}\]
複素振幅反射率
薄膜に入射した電場、磁場と薄膜から反射した電場、磁場の複素振幅の比である。
\(n_2,~ k_z\) 等の定義は上記と同じ。
繰り返すが、 \(n_2\) の定義によってはこれの複素共役を用いる必要がある。
\[ \begin{equation}
\left\{
\def\nAcosineA{\sqrt{n_{1}^{2}-\sin ^{2} \theta_{0}}}
\def\nBcosineB{\sqrt{n_{2}^{2}-\sin ^{2} \theta_{0}}}
\def\nAcosineAsq{(n_{1}^{2}-\sin ^{2} \theta_{0})}
\def\nBcosineBsq{(n_{2}^{2}-\sin ^{2} \theta_{0})}
\def\nAsq{n_{1}^{2}}
\def\nBsq{n_{2}^{2}}
\def\nAsqsq{n_{1}^{4}}
\def\nBsqsq{n_{2}^{4}}
\def\eplus{\exp{(ik_{z}d)}}
\def\eminus{\exp{(-ik_{z}d)}}
\begin{array}{l}
r_{s}=\frac{E2}{E1}=\frac{[\nAcosineAsq - \nBcosineBsq] [\eplus-\eminus]}{(\nAcosineA+\nBcosineB)^{2}\eplus - (\nAcosineA-\nBcosineB)^{2}\eminus}\\
r_{p}=\frac{H2}{H1}=\frac{[\nBsqsq \nAcosineAsq)-\nAsqsq \nBcosineBsq] [\eplus-\eminus]}{(\nBsq \nAcosineA+\nAsq \nBcosineB)^{2}\eplus - (\nBsq \nAcosineA - \nAsq \nBcosineB)^{2} \eminus}
\end{array}
\right.
\end{equation}\]
計算する際に便利な表式
実際に計算する際には、数式が長いと間違えやすい。以下のような書き換えが便利である。
\[ \begin{equation}
\left\{
\begin{array}{l}
\left(
\begin{array}{l}
n_{1}{\rm :~~real}\\
n_{2}=n-i\kappa\\
k_{0}{\rm :~~angular~~wavenumber~~in~~vacuum}\\
k_{z}=k_{0}\nBcosineB
\end{array}
\right){\rm 再掲}
\\
\alpha=\nAcosineA\\
\beta=\nBcosineB\\
\alpha'=\frac{\nAcosineA}{n_{1}^{2}}\\
\beta' = \frac{\nBcosineB}{n_{2}^{2}}\\
t_{s}=\frac{E5}{E1}=\frac{4 \alpha \beta}{(\alpha +\beta)^{2}\exp{(ik_{z}d)} - (\alpha-\beta)^{2}\exp{(-ik_{z}d)}}\\
t_{p}=\frac{H5}{H1}=\frac{4 \alpha' \beta'}{(\alpha' +\beta')^{2}\exp{(ik_{z}d)} - (\alpha'-\beta')^{2}\exp{(-ik_{z}d)}}\\
r_{s}=\frac{E2}{E1}=\frac{(\alpha^{2}-\beta^{2})(\eplus-\eminus)}{(\alpha+\beta)^{2}\eplus-(\alpha-\beta)^{2}\eminus}\\
r_{p}=\frac{H2}{H1}=\frac{(\alpha'^{2}-\beta'^{2})(\eplus-\eminus)}{(\alpha'+\beta')^{2}\eplus-(\alpha'-\beta')^{2}\eminus}
\end{array}
\right.
\end{equation}\]




